Waterhammer from Valve Operation
When a valve is being opened or closed to change the flow rate, the change in kinetic energy of the flowing fluid column introduces a transient change in the static pressure in the pipe. In the case of a liquid, this transient change in the static pressure is sometimes accompanied by a shaking of the pipe and a hammering sound—thus the name waterhammer.
The transient pressure change does not occur instantaneously along the entire pipeline but progressively from the point at which the change of flow has been initiated. If, for example, a valve at the end of a pipeline is closed instantaneously, only the liquid elents at the valve feel the valve closure immediately. The kinetic energy stored in the liquid elents then compresses these elents and expands the adjoining pipe walls. The other portion of the liquid column continues to flow at its original velocity until reaching the liquid column which is at rest.
The speed at which the compression zone extends towards the inlet end of the pipeline is uniform and equals the velocity of sound in the liquid within the pipe. When the compression zone has reached the inlet pipe end, all liquid is at rest, but at a pressure above the normal static pressure. The unbalanced pressure now creates a flow in the opposite direction and relieves the rise in the static pressure and the expansion of the pipe wall. When this pressure drop has reached the valve, the whole liquid column is again under normal static pressure, but continues to discharge towards the inlet pipe end so that a wave of subnormal pressure is created, starting at the valve. When this pressure wave has made the roundtrip, the normal pressure and the original direction of flow are restored. Now the cycle starts again and repeats itself until the kinetic energy of the liquid column is dissipated in friction and other losses.
Joukowsky has shown that instantaneous valve closure raises the static pressure in the pipeline by:
![]()
where
ΔP = rise in pressure above normal
v = velocity of a rested flow
a = velocity of pressure wave propagation
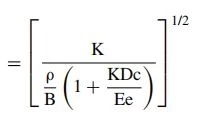
ρ = density of the liquid
K = bulk modulus of the liquid
E = Young’s modulus of elasticity of the pipe wall material D = inside diameter of pipe
e = thickness of pipe wall
c = pipe restriction factor (c = 1.0 for unrestricted piping)
B (SI units) = 1.0
B (imperial units, fps) = g = 32.174 ft/s2
In the case of steel piping with a D/e ratio of 35 and water flow, the pressure wave travels at a velocity of approximately 1200 m/s (about 4000 ft/s), and the static pressure increases by 13.5 bar for each 1 m/s, or about 60 lb/in2 for each 1 ft/s instantaneous velocity change.
If the valve does not close instantaneously but within the time of a pressure-wave roundtrip of 2L/a, where Listhe length of the pipeline, the first returning pressure wave cannot cancel the last outgoing pressure wave, and the pressure rise is the same as if the valve were closed instantaneously. This speed of closure is said to be rapid.
If the valve takes longer to close than 2L/a, the returning pressure waves cancel a portion of the outgoing waves so that the maximum pressure rise is reduced. This speed of closure is said to be slow.
To minimize the formation of unduly high surge pressures from opening or closing valves, stop valves should be operated slowly and in a manner that produces a uniform rate of change of the flow velocity. Check valves, however, are operated by the flowing fluid, and their speed of closure is a function of the valve design and the deceleration characteristic of the retarding fluid column.
If the surge pressure is due to a pump stopping, the calculation of the surge pressure must take into account the pump characteristic and the rate of change of the pump speed after the power supply has been cutoff.
If the distance between the check valve and the point of pressure wave reflectionis long, and the elevation and the pressure at this point are low, the syst tolerates a slow-closing check valve. On the other hand, if the distance between the check valve and the point of reflectionis short, and the pressure at this point is high, the flow reverses almost instantaneously and the check valve must be able to close extrely fast. Such nearly instantaneous reverse flow occurs, for example, in multipump installations in which one pump fails suddenly. Guidelines on the selection of check valves for speed of closure are given in Chapter 4.
Calculation of the fluid pressure and velocity as a function of time and location along a pipe can be accomplished in several ways. For simple cases, graphical and algebraic methods can be used. However, the ready availability of digital computers has made the use of numer- ical methods convenient and allows solutions to any desired accuracy to be obtained. See Reference 25 for a description of this calculating method.
In some cases it maybe impossible or impractical to reduce the effects of waterhammer by adjusting the valve characteristic. Consideration should then be given to changing the characteristic of the piping syst. One of the most common ways of achieving this is to incorporate one or more surge protection devices at strategic locations in the piping syst. Such devices may consist of a standpipe containing gas indirect contact with the liquid or separated from the liquid by a flexiblewall or a pressure relief valve.
The effects of waterhammer may also be altered by deliberately changing the acoustic properties of the fluid. This can be done, for example, by introducing bubbles of a non-dissolvable gas directly into the fluid stream. The effect of this is to reduce the effective density and bulk modulus of the fluid. A similar effect can be achieved if the gas is enclosed in a flexible walled conduit, or hose, which runs the length of the pipe.
If even a small amount of gas is present, the effect of pipe wall elasticity in Equation 2-26 becomes insignificant, and the modified acoustic velocity may be expressed by:

where
K = modified fluid bulk modulus

B = 1.0 (coherent SI units)
B = 32.174 ft/s2 (imperial units, fps)
Kg = bulk modulus of gas
Kl = bulk modulus of liquid
Vg = volume of gas
Vl = volume of liquid
Vt = total volume
ρg = density of gas
ρl = density of liquid
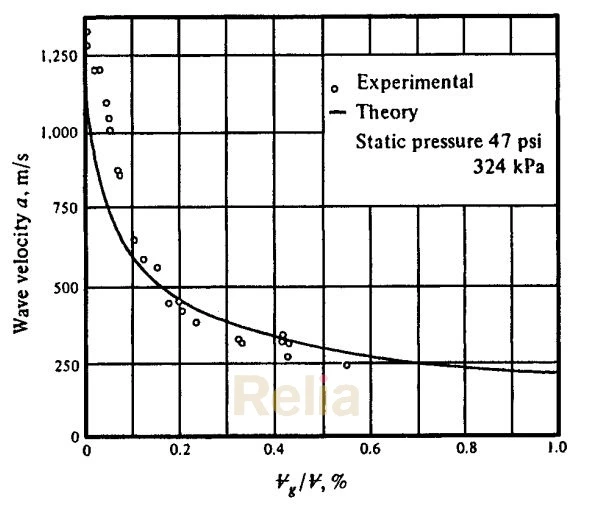
Figure 2-12. Propagation Velocity α of a Pressure Wave in Pipeline for Varying Air Content (Theoretical and Experimental Results).26 Reprint from Fluid Transients by E. B. Wylie and V. L Streeter, by courtesy of the authors.
Figure 2-12 shows the effect of air content on the wave propagation velocity in water. Note that a small amount of air content produces a wave speed less than the speed of sound in air, which, for dry air at 20℃ (68℉) and atmospheric pressure, is 318 m/s (1042 ft/s).



